

A third order polydispersity index may also be derived but this is only necessary if the particles of the system are highly polydisperse.

Where is the average decay rate and is the second order polydispersity index (or an indication of the variance). One of the most common methods is the cumulant method, from which in addition to the sum of the exponentials above, more information can be derived about the variance of the system as follows: The simplest approach is to treat the first order autocorrelation function as the sum of single exponential decays with fractions where is the decay rate. Once the autocorrelation curve has been generated, different mathematical approaches can be employed to fit the curve and thus determine the z-averaged translational diffusion coefficient. Where is a parameter which is a correction factor depending on the geometry and alignment of the laser beam of the light scattering setup it is roughly equal to the inverse of the number of speckle (see Speckle pattern) from which light is collected. The Siegert equation, relates the second order autocorrelation curve with the first order autocorrelation function as follows: If the sample was monodisperse the decay would simply be a single exponential. the autocorrelation function), numerical methods are used based on calculations of assumed distributions. This exponential decay is obviously then related to the motion of the particles specifically, the diffusion coefficient. As the time delays become longer, the correlation starts to exponentially fall off to zero, meaning that there is no correlation between the intensity of scattering of the initial state with the final state after a long time period has elapsed (relative to the motion of the particles).
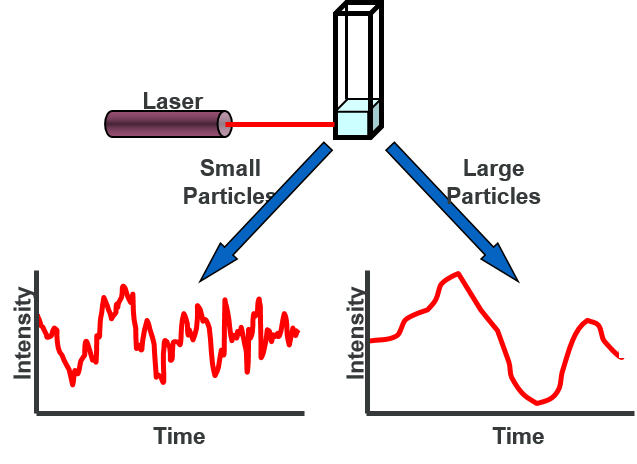
The two signals are thus essentially unchanged when compared after only a very short time interval. At short time delays the correlation is high because the particles do not have a chance to move to a great extent from the initial state that they were in. Where is the autocorrelation function at a particular wave vector, and delay time, and is the intensity. The second order autocorrelation curve is generated from the intensity trace as follows: The dynamic information of the particles is derived from an autocorrelation of the intensity trace recorded during the experiment. One of such methods is dynamic light scattering, also known as quasi elastic laser light scattering. There are several ways to derive dynamic information about particles’ movement in solution by Brownian motion. This scattered light then undergoes either constructive or destructive interference by the surrounding particles and within this intensity fluctuation information is contained about the time scale of movement of the scatterers. These fluctuations are due to the fact that the small molecules in solutions are undergoing Brownian motion and so the distance between the scatterers in the solution is constantly changing with time. If the light source is a laser, and thus is monochromatic and coherent, then one observes a time-dependent fluctuation in the scattering intensity. When light hits small particles the light scatters in all directions (Rayleigh scattering) so long as the particles are small compared to the wavelength (< 250 nm).


 0 kommentar(er)
0 kommentar(er)
